Учебные пособия > College Algebra
The product is a quadratic expression. Set equal to zero, [latex]^+x - 6=0[/latex] is a quadratic equation. If we were to factor the equation, we would get back the factors we multiplied. The process of factoring a quadratic equation depends on the leading coefficient, whether it is 1 or another integer. We will look at both situations; but first, we want to confirm that the equation is written in standard form, [latex]a^+bx+c=0[/latex], where a, b, and c are real numbers, and [latex]a\ne 0[/latex]. The equation [latex]^+x - 6=0[/latex] is in standard form. We can use the zero-product property to solve quadratic equations in which we first have to factor out the greatest common factor (GCF), and for equations that have special factoring formulas as well, such as the difference of squares, both of which we will see later in this section.
A General Note: The Zero-Product Property and Quadratic Equations
The zero-product property states
[latex]\texta\cdot b=0,\text< then >a=0\text< or >b=0[/latex],
where a and b are real numbers or algebraic expressions. A quadratic equation is an equation containing a second-degree polynomial; for example
[latex]a^+bx+c=0[/latex]
where a, b, and c are real numbers, and if [latex]a\ne 0[/latex], it is in standard form.
Solving Quadratics with a Leading Coefficient of 1
In the quadratic equation [latex]^+x - 6=0[/latex], the leading coefficient, or the coefficient of [latex]^[/latex], is 1. We have one method of factoring quadratic equations in this form.
How To: Given a quadratic equation with the leading coefficient of 1, factor it.
- Find two numbers whose product equals c and whose sum equals b.
- Use those numbers to write two factors of the form [latex]\left(x+k\right)\text< or >\left(x-k\right)[/latex], where k is one of the numbers found in step 1. Use the numbers exactly as they are. In other words, if the two numbers are 1 and [latex]-2[/latex], the factors are [latex]\left(x+1\right)\left(x - 2\right)[/latex].
- Solve using the zero-product property by setting each factor equal to zero and solving for the variable.
Example 1: Factoring and Solving a Quadratic with Leading Coefficient of 1
Factor and solve the equation: [latex]^+x - 6=0[/latex].
Solution
To factor [latex]^+x - 6=0[/latex], we look for two numbers whose product equals [latex]-6[/latex] and whose sum equals 1. Begin by looking at the possible factors of [latex]-6[/latex].
[latex]\begin1\cdot \left(-6\right)\hfill \\ \left(-6\right)\cdot 1\hfill \\ 2\cdot \left(-3\right)\hfill \\ 3\cdot \left(-2\right)\hfill \end[/latex]
The last pair, [latex]3\cdot \left(-2\right)[/latex] sums to 1, so these are the numbers. Note that only one pair of numbers will work. Then, write the factors.
[latex]\left(x - 2\right)\left(x+3\right)=0[/latex]
To solve this equation, we use the zero-product property. Set each factor equal to zero and solve.
[latex]\begin\left(x - 2\right)\left(x+3\right)\hfill&=0\hfill \\ \left(x - 2\right)\hfill&=0\hfill \\ x\hfill&=2\hfill \\ \left(x+3\right)\hfill&=0\hfill \\ x\hfill&=-3\hfill \end[/latex]
The two solutions are [latex]x=2[/latex] and [latex]x=-3[/latex]. We can see how the solutions relate to the graph in Figure 2. The solutions are the x-intercepts of the function [latex]f(x) = ^+x - 6[/latex].
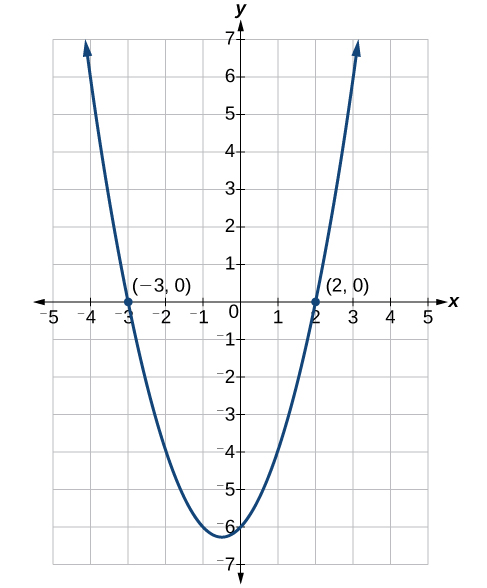
Figure 2
Try It 1
Factor and solve the quadratic equation: [latex]^-5x - 6=0[/latex]. Solution
Example 2: Solve the Quadratic Equation by Factoring
Solve the quadratic equation by factoring: [latex]^+8x+15=0[/latex].
Solution
Find two numbers whose product equals [latex]15[/latex] and whose sum equals [latex]8[/latex]. List the factors of [latex]15[/latex].
[latex]\begin1\cdot 15\hfill \\ 3\cdot 5\hfill \\ \left(-1\right)\cdot \left(-15\right)\hfill \\ \left(-3\right)\cdot \left(-5\right)\hfill \end[/latex]
The numbers that add to 8 are 3 and 5. Then, write the factors, set each factor equal to zero, and solve.
[latex]\begin\left(x+3\right)\left(x+5\right)\hfill&=0\hfill \\ \left(x+3\right)\hfill&=0\hfill \\ x\hfill&=-3\hfill \\ \left(x+5\right)\hfill&=0\hfill \\ x\hfill&=-5\hfill \end[/latex]
The solutions are [latex]x=-3[/latex] and [latex]x=-5[/latex].
Try It 2
Solve the quadratic equation by factoring: [latex]^-4x - 21=0[/latex]. Solution
Example 3: Using the Zero-Product Property to Solve a Quadratic Equation Written as the Difference of Squares
Solve the difference of squares equation using the zero-product property: [latex]^-9=0[/latex].
Solution
Recognizing that the equation represents the difference of squares, we can write the two factors by taking the square root of each term, using a minus sign as the operator in one factor and a plus sign as the operator in the other. Solve using the zero-factor property.
[latex]\begin^-9=0\hfill \\ \left(x - 3\right)\left(x+3\right)=0\hfill \\ \hfill \\ \left(x - 3\right)=0\hfill \\ x=3\hfill \\ \hfill \\ \left(x+3\right)=0\hfill \\ x=-3\hfill \end[/latex]
The solutions are [latex]x=3[/latex] and [latex]x=-3[/latex].
Try It 3
Solve by factoring: [latex]^-25=0[/latex]. Solution
Factoring and Solving a Quadratic Equation of Higher Order
- With the quadratic in standard form, [latex]a^+bx+c=0[/latex], multiply [latex]a\cdot c[/latex].
- Find two numbers whose product equals [latex]ac[/latex] and whose sum equals [latex]b[/latex].
- Rewrite the equation replacing the [latex]bx[/latex] term with two terms using the numbers found in step 1 as coefficients of x.
- Factor the first two terms and then factor the last two terms. The expressions in parentheses must be exactly the same to use grouping.
- Factor out the expression in parentheses.
- Set the expressions equal to zero and solve for the variable.
Example 4: Solving a Quadratic Equation Using Grouping
Use grouping to factor and solve the quadratic equation: [latex]4^+15x+9=0[/latex].
Solution
First, multiply [latex]ac:4\left(9\right)=36[/latex]. Then list the factors of [latex]36[/latex].
[latex]\begin1\cdot 36\hfill \\ 2\cdot 18\hfill \\ 3\cdot 12\hfill \\ 4\cdot 9\hfill \\ 6\cdot 6\hfill \end[/latex]
The only pair of factors that sums to [latex]15[/latex] is [latex]3+12[/latex]. Rewrite the equation replacing the b term, [latex]15x[/latex], with two terms using 3 and 12 as coefficients of x. Factor the first two terms, and then factor the last two terms.
[latex]\begin4^+3x+12x+9=0\hfill \\ x\left(4x+3\right)+3\left(4x+3\right)=0\hfill \\ \left(4x+3\right)\left(x+3\right)=0\hfill \end[/latex]
Solve using the zero-product property.
[latex]\begin\left(4x+3\right)\left(x+3\right)=0\hfill \\ \hfill \\ \left(4x+3\right)=0\hfill \\ x=-\frac\hfill \\ \hfill \\ \left(x+3\right)=0\hfill \\ x=-3\hfill \end[/latex]
The solutions are [latex]x=-\frac<3>[/latex], [latex]x=-3[/latex].
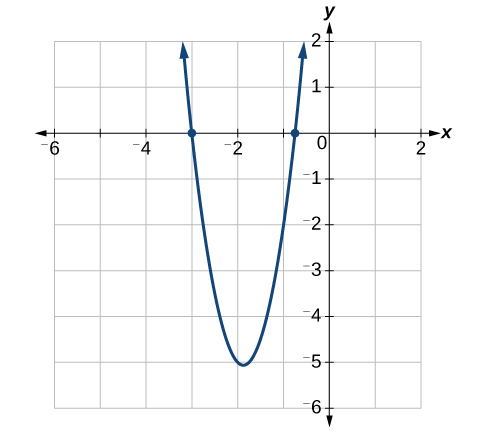
Figure 3
Try It 4
Solve using factoring by grouping: [latex]12^+11x+2=0[/latex]. Solution
Example 5: Solving a Higher Degree Quadratic Equation by Factoring
Solve the equation by factoring: [latex]-3^-5^-2x=0[/latex].
Solution
This equation does not look like a quadratic, as the highest power is 3, not 2. Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out [latex]-x[/latex] from all of the terms and then proceed with grouping.
[latex]\begin-3^-5^-2x=0\hfill \\ -x\left(3^+5x+2\right)=0\hfill \end[/latex]
Use grouping on the expression in parentheses.
[latex]\begin-x\left(3^+3x+2x+2\right)=\hfill&0\hfill \\ -x\left[3x\left(x+1\right)+2\left(x+1\right)\right]=\hfill&0\hfill \\ -x\left(3x+2\right)\left(x+1\right)=\hfill&0\hfill \end[/latex]
Now, we use the zero-product property. Notice that we have three factors.
[latex]\begin-x\hfill&=0\hfill \\ x\hfill&=0\hfill \\ 3x+2\hfill&=0\hfill \\ x\hfill&=-\frac\hfill \\ x+1\hfill&=0\hfill \\ x\hfill&=-1\hfill \end[/latex]
The solutions are [latex]x=0[/latex], [latex]x=-\frac<2>[/latex], and [latex]x=-1[/latex].
Try It 5
Solve by factoring: [latex]^+11^+10x=0[/latex]. Solution
Licenses & Attributions
CC licensed content, Specific attribution
- College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/[email protected]:1/Preface. License:CC BY: Attribution.



